Muita gente acha que matemática é só fazer contas e aplicar fórmulas pré-definidas para obter resultados numéricos sobre situações-problema inventadas pelos professores. Grande e triste engano. Embora fazer contas seja, sim, uma parte significativa da matemática, essa parte é tão pequena que o matemático profissional às vezes até se esquece dela. Parece brincadeira, mas é muito comum, na pesquisa acadêmica, professores de matérias avançadas provarem teoremas complicadíssimos e se embananarem por alguns segundos na hora de resolver continhas triviais como 7x8 ou 4x13, por exemplo. No fundo, ninguém se importa com isso, porque todo mundo sabe que a essência de um matemático não é ser rápido em fazer contas, mas, sim, ter espírito investigativo e um intelecto ousado para procurar descobrir verdades abstratas sobre o mundo que nos rodeia. Um computador pode fazer uma conta difícil (e com rapidez e precisão infinitamente maiores do que a de qualquer ser humano), mas foram necessários seres humanos com espírito matemático aguçado para desenvolver as bases científicas e teóricas necessárias para a construção dos computadores.
Para acabar com essa visão equivocada, vou dar um exemplo bastante simples para proporcionar uma noção sobre o que a matemática de fato é.
Como
qualquer estudante de ensino médio sabe, muitos dos problemas que surgem no dia-a-dia
das pessoas e, ainda mais, nas questões práticas dos profissionais que lidam com
o mundo físico (engenheiros, programadores, químicos, peritos, etc.) podem ser
descritos pelas tão famosas equações de segundo grau. A curvatura de certas
estruturas arquitetônicas, o formato de um arco-íris, a aceleração de um corpo
ou partícula (uma bala de revólver ou um carro em movimento, por exemplo),
entre inúmeros outros fenômenos, acabam gerando expressões do segundo grau.
Para quem
não se lembra, uma expressão do
segundo grau é algo como x² –4x + 3,
tornando-se uma equação do segundo
grau quando igualamos isso a zero: x²
– 4x + 3 = 0. (O nome “do segundo
grau” vem do fato de que a incógnita “x” está elevada à segunda potência).
No primeiro
caso, a expressão pode assumir
diversos valores, cada um dependendo do valor que a gente escolher para x. Por
exemplo, para x = 2, temos:
x² – 4x + 3
= 2² – 4.2 + 3 = 4 – 8 + 3 = –1
Para x = 3,
temos:
x² – 4x + 3
= 3² – 4.3 + 3 = 9 – 12 + 3 = 0
No segundo caso, a equação
x² – 4x + 3 = 0 é uma notação que utilizamos para que possamos descobrir qual
valor de x no dará que a expressão x² – 4x + 3 resulte no valor 0. Como já
vimos, para x = 3 teremos que x² – 4x + 3 é zero, então x = 3 é uma solução
para a equação x² – 4x + 3 = 0.
Contudo, como vamos saber se essa é a única solução possível?
Será que não existem outras? Se sim, como vou descobri-las? Se não, como
poderei ter certeza? Eu não posso passar minha vida inteira testando números
para descobrir isso a fim de solucionar um único problema (mesmo porque os
números são infinitos, de modo que minha vida seria insuficiente para ficar
testando um a um).
É aí que entra o grande lance da matemática.
Como alguém, algum dia, percebeu que existe uma enorme gama
de problemas práticos que precisam ser resolvidos por meio de equações de
segundo grau, alguma pessoa teve a ideia brilhante de generalizar TODAS as equações de segundo grau e desenvolver métodos
para fazer afirmações SEGURAMENTE VERDADEIRAS a respeito dessas equações.
O que antes era um problema específico do tipo “x² – 4x + 3 =
0” se tornou um assunto muito mais geral e abstrato, um assunto que já não tem
mais nada a ver com a curvatura de um monumento ou a forma de um arco-íris.
Trata-se, agora, de um problema puramente matemático.
Assim, o matemático, ao invés de trabalhar com uma equação
com valores numéricos, como a do exemplo acima, resolveu generalizar e
trabalhar com símbolos no lugar dos números. Por facilidade, optou por chamar
os números de “a”, “b” e “c”, fazendo essas letras representarem números quaisquer.
Assim, a forma mais geral possível de uma equação do segundo
grau é "ax² + bx + c = 0", onde “a”, “b” e “c” são números conhecidos e “x” é o valor
que queremos descobrir.
Trabalhando dessa maneira abstrata e sem as limitações de
valores específicos, os matemáticos conseguiram descobrir muitas e muitas
coisas a respeito dessas equações. Por exemplo: toda equação de segundo grau terá
no máximo duas soluções, nunca três, quatro ou cinco. E essas soluções podem
ser encontradas por meio de uma fórmula (a famosa “fórmula de Bháskara”) que
funciona absolutamente SEMPRE, em todos os casos, para quaisquer valores de “a”,
“b” e “c”. Com isso, não apenas a equação “x² – 4x + 3 = 0” se tornou “solucionável”,
mas também a equação “500x² + 12x – 20 = 0”, a equação “(18π)x² - 17ex = (13 +
12x²)/15” e infinitas outras.
 |
| A famosa (e injustamente temida) "fórmula de Bháskara" |
A fórmula, ao contrário do que os professores do ensino
fundamental fazem parecer, não foi “inventada” por alguém, mas, sim, descoberta por meio de raciocínios
dedutivos que garantiram a total veracidade do procedimento.
Claro que eu não vou demonstrar a validade da fórmula aqui
(embora essa demonstração seja bastante simples), porque não é o momento
adequado (para os interessados, contudo, acrescentei a demonstração no final deste artigo, como um bônus). O ponto que quero
evidenciar é que um processo que aparentemente tornava o problema muito mais
complicado (substituir os números por letras e generalizá-lo para todas as
equações de segundo grau) foi justamente o que proporcionou novas descobertas
sobre o assunto e garantiu o progresso de inúmeras ciências.
Encontrar os valores de x e poder dizer quantas soluções cada
equação terá são apenas algumas das dezenas de descobertas que se fizeram a
partir daí. A álgebra se desenvolveu e hoje sabemos que cada equação de grau “n”
(sendo “n” um número natural qualquer: 1, 2, 3, 4, 5, ...) tem no máximo “n”
soluções distintas.
E tudo isso proporcionou que as pessoas que trabalham com
questões práticas obtivessem novas ferramentas para resolver seus problemas,
podendo realizar obras mais interessantes, fazer serviços mais acurados,
construir invenções mais inovadoras.
Televisão, telefone, computador, internet, automóveis,
celulares... Agradeça por essas tecnologias a seus inventores, é claro, mas,
antes, agradeça a um matemático!
E uma última curiosidade: a matemática sempre depende de uma
prova rigorosa e absoluta de seus resultados. O teorema de Pitágoras, por
exemplo, já era conhecido por algumas civilizações muito antes do nascimento de
Pitágoras (mas sem esse nome, é claro), mas ninguém sabia como garantir que ele valia em todos os casos possíveis. Para realizar medições e fazer
construções, as pessoas percebiam que, num triângulo-retângulo, a medida do comprimento da
hipotenusa elevada ao quadrado equivale à soma dos quadrados dos comprimentos dos
catetos. Contudo, ninguém tinha certeza se isso valia sempre. Essa certeza dependia de uma demonstração rigorosa que servisse para todos os triângulos-retângulos. E Pitágoras foi (acredita-se) o
primeiro a encontrar essa prova absoluta. Daí decorre sua importância.
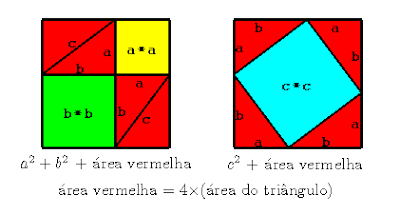 |
| Esboço de uma demonstração do teorema de Pitágoras. |
Bônus:
Para as pessoas que já possuam uma maior familiaridade com a álgebra, resolvi registrar aqui uma demonstração sucinta, sem grandes explicações, da fórmula de Bháskara (coisa que nunca nos apresentam na escola!).
Sejam a, b e c números reais conhecidos.
Considere ax² + bx
+ c = 0
Multiplicando 4a nos dois lados da igualdade, teremos que
4a²x² + 4abx + 4ac = (4a).0
Ou seja
4a²x² + 4abx + 4ac = 0 ⇒
4a²x² + 4abx = –4ac
Somando b² nos dois lados, obtemos
4a²x² + 4abx + b² = b² – 4ac
Note que 4a²x² + 4abx
+ b² é um quadrado perfeito que pode ser reescrito como (2ax + b)². Logo
4a²x² + 4abx + b² = b² – 4ac ⇒
(2ax + b)² = b² – 4ac
Extraindo a raiz quadrado dos dois lados, temos que
E, portanto,
Daí decorre naturalmente que
Que é o que queríamos provar.



Nenhum comentário:
Postar um comentário